Le problème

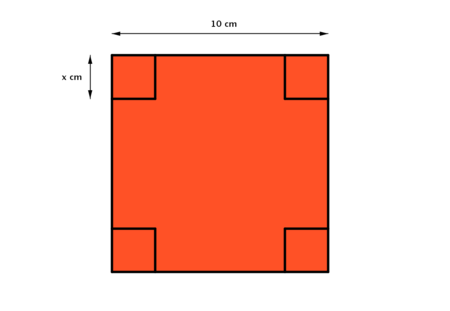
On considère un carré de côté 10 cm.
À chaque coin de ce carré, on découpe un carré de côté $x$ cm.
On obtient alors le patron d’une boîte parallélépipédique sans couvercle.
On cherche la ou les valeurs de $x$ pour que le volume de cette boîte soit égal à 70 cm³.

Mise en équation

Comme dans chaque coin on découpe un carré de côté $x$ cm, on a :

$$0< x <5$$

Le volume d’un parallélépipède rectangle est le produit $longueur \times largeur \times hauteur$.

Ici $longueur = largeur=(10-2x)$ et $hauteur =x$.

Donc le volume de la boîte est donné par :

$$V =x(10-2x)^2$$

Donc pour trouver la ou les valeurs de $x$ pour que le volume de cette boîte soit égal à 70 cm³, on doit résoudre l’équation :

$$x(10-2x)^2 =70$$

On développe le membre de gauche :

$$x(100-40x+4x^2) =70$$

$$4x^3-40x^2+100x =70$$

On dit que c’est une équation de degré 3 (à cause du $x ^3$).

On utilise le tableur pour associer à plusieurs valeurs de $x$ le volume $V$ correspondant.

Le volume $V$ change de valeur quand $x$ change. Le volume $V$ dépend donc de la valeur de $x$. On notera donc le volume $V (x)$ (prononcer "$V$ de $x$").

Résolution de l’équation

En utilisant un tableur on obtient la courbe suivante :

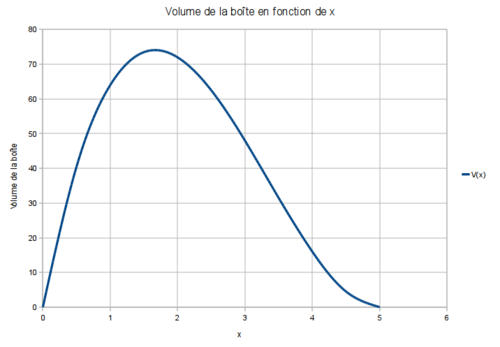
Les solutions de l’équation sont les abscisses des points de la courbe ayant pour ordonnée 70.

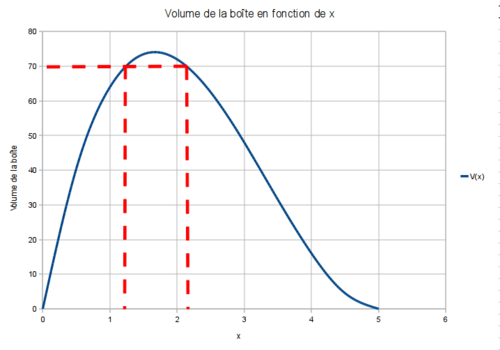
On peut lire 1,3 et 2,2, qui sont des valeurs approchées des solutions.