Problèmes de synthèse sur la symétrie axiale

mercredi 6 mai 2009
par  Classe de Mathématiques 1

- Ci-dessous, construis un triangle ABC rectangle en B tel que AB = 5 cm et \widehat{BAC}=30°
, puis le cercle (c) de centre B et de rayon AB.

- Construis le point B’, symétrique de B par rapport à la droite (AC).

- Construis le symétrique du cercle (c).

- Quelle est la nature du triangle AB’C ? (énonce la propriété du cours correspondante).

Solution {JPEG}

  1. Tracez une droite (d) oblique, sans vous aider du quadrillage.
    Placez un point A d’un côté de (d) et un point B de l’autre côté de (d).
  2. Construisez avec l’équerre le symétrique de A par rapport à (d) en laissant les traces de construction.
  3. Construisez avec le compas le symétrique de B par rapport à (d) en laissant les traces de construction.
  4. Quelle est l’image du segment [AB] par la symétrie d’axe (d) ? (Répondez par une phrase.)
  5. Comparez la longueur des segments [A’B’] et [AB]. (Répondez par une phrase et justifiez par une propriété du cours.)

Solution {JPEG}

  1. Construisez un triangle ABC rectangle en B tel que AB = 5 cm et BC = 3 cm,
  2. Sur la même figure, tracez le cercle (ℓ) de centre B et de rayon [BC].
  3. Tracez une droite (d) oblique qui ne coupe ni le triangle ABC, ni le cercle (ℓ).
  4. Par la méthode de votre choix, construisez le symétrique du triangle ABC par rapport à (d).
  5. Calculez l’aire du triangle ABC.
  6. Sans aucun calcul et en justifiant par une phrase, donnez l’aire du triangle A’B’C’.
  7. Question facultative : construisez l’image (ℓ’) de (ℓ) par la symétrie d’axe (d) puis calculez le périmètre du cercle (ℓ’).

Solution {JPEG}


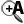
Commentaires

Navigation

Articles de la rubrique