Théorème de Thalès : démonstration

vendredi 23 mai 2003
par  professeur de Mathématiques 1

La première démonstration du théorème de Thalès est due à Euclide, dans
le livre VI de ses Éléments. Nous nous proposons de la restituer en
langage moderne...

 

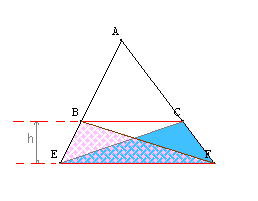
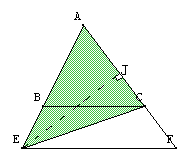
Les aires des triangles BEF et CEF sont égales (et valent toutes deux $\frac{EF \times h}{2}$)

 

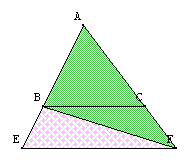
 Or $aire(ABF)=aire(AEF)-aire(BEF)$

 

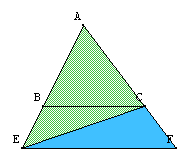
et de même : $aire(ACE) = aire(AEF)-aire(CEF)$

Donc $aire(ABF) = aire(ACE)$

Nous allons exploiter ces égalités sur les aires.

 

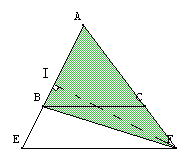
En utilisant la hauteur (FI), on trouve que :

  • $aire(ABF) = \frac{AB \times FI}{2}$
  • $aire(AEF) = \frac{AE \times FI}{2}$

On a donc : $\frac{aire(ABF)}{aire(AEF)} = \frac{AB}{AE}$ (1)

 

De même, en utilisant la hauteur (EJ), on trouve :

$\frac{aire(ACE)}{aire(AEF)} = \frac{AC}{AF}$ (2)

Mais (1) et (2) sont égales, et on trouve le théorème
de Thalès.

Source : https://www.bibmath.net/


Commentaires